I have implemented my own version, also based on the threejs CatmullRomCurve3.js like @sable did.
But I didn’t base it off of @sable since I had already started on it and figured it was easier to complete what I already had, but again, thanks for your sharing, I appreciate it.
My version works with the current version of BabylonJS, and it’s written in TypeScript.
Here is the code:
import * as BABYLON from "@babylonjs/core";
/**
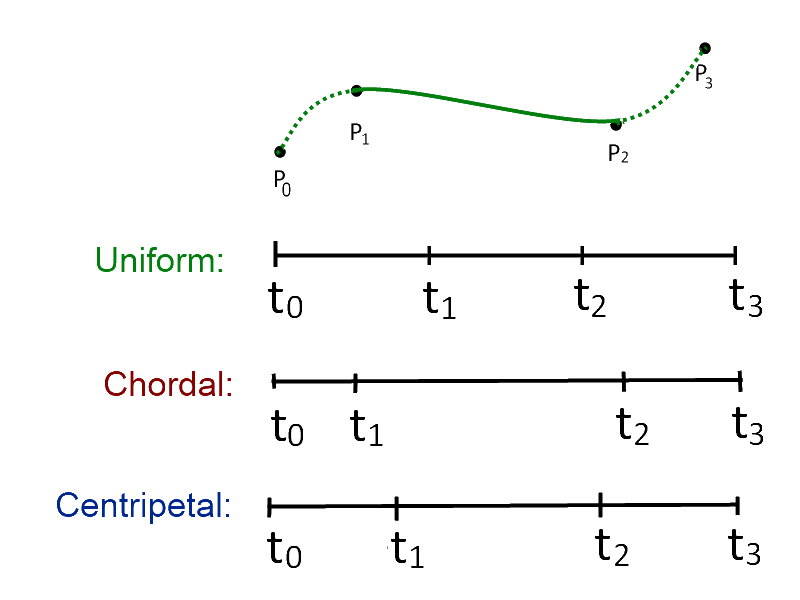
* Centripetal CatmullRom Curve - which is useful for avoiding
* cusps and self-intersections in non-uniform catmull rom curves.
* http://www.cemyuksel.com/research/catmullrom_param/catmullrom.pdf
*
* curve.type accepts centripetal(default), chordal and catmullrom
* curve.tension is used for catmullrom which defaults to 0.5
*/
/*
Based on an optimized c++ solution in
- http://stackoverflow.com/questions/9489736/catmull-rom-curve-with-no-cusps-and-no-self-intersections/
- http://ideone.com/NoEbVM
This CubicPoly class could be used for reusing some variables and calculations,
but for three.js curve use, it could be possible inlined and flatten into a single function call
which can be placed in CurveUtils.
*/
interface CubicPoly {
initCatmullRom(x0: number, x1: number, x2: number, x3: number, tension: number): void;
initNonuniformCatmullRom(x0: number, x1: number, x2: number, x3: number, dt0: number, dt1: number, dt2: number, tension : number): void;
calc(t: number): number;
}
class CubicPoly implements CubicPoly {
c0: number;
c1: number;
c2: number;
c3: number;
constructor() {
this.c0 = 0;
this.c1 = 0;
this.c2 = 0;
this.c3 = 0;
}
initCatmullRom(x0: number, x1: number, x2: number, x3: number, tension: number) {
this.init(x1, x2, tension * (x2 - x0), tension * (x3 - x1));
}
initNonuniformCatmullRom(x0: number, x1: number, x2: number, x3: number, dt0: number, dt1: number, dt2: number, tension: number) {
// compute tangents when parameterized in [t1,t2]
let t1 = (x1 - x0) / dt0 - (x2 - x0) / (dt0 + dt1) + (x2 - x1) / dt1;
let t2 = (x2 - x1) / dt1 - (x3 - x1) / (dt1 + dt2) + (x3 - x2) / dt2;
// rescale tangents for parametrization in [0,1]
t1 *= dt1 * (tension);
t2 *= dt1 * (tension);
this.init(x1, x2, t1, t2);
}
calc(t: number) {
const t2 = t * t;
const t3 = t2 * t;
return this.c0 + this.c1 * t + this.c2 * t2 + this.c3 * t3;
}
init(x0: number, x1: number, t0: number, t1: number) {
this.c0 = x0;
this.c1 = t0;
this.c2 = -3 * x0 + 3 * x1 - 2 * t0 - t1;
this.c3 = 2 * x0 - 2 * x1 + t0 + t1;
}
}
//
const px = new CubicPoly();
const py = new CubicPoly();
const pz = new CubicPoly();
class CatmullRomCurve3 {
isCatmullRomCurve3 : boolean;
type : string;
closed : boolean;
curveType : string;
tension : number;
curve: BABYLON.Curve3;
nbPoints : number;
constructor( points : BABYLON.Vector3[], nbPoints : number, closed = false, curveType = 'centripetal', tension = 0.5 ) {
// super(points);
Object.assign(this, new BABYLON.Curve3(points));
this.curve = new BABYLON.Curve3(points);
this.isCatmullRomCurve3 = true;
this.type = 'CatmullRomCurve3';
this.closed = closed;
this.curveType = curveType;
this.tension = tension;
this.nbPoints = nbPoints;
}
// My own override of the original getPoints behaviour,
// This one uses nbPoints... goes through all steps
getPoints(){
const rawPoints = this.curve.getPoints();
const result = [];
for(let i = 0; i < rawPoints.length; i += rawPoints.length / this.nbPoints){
result.push( this.getPoint(i / rawPoints.length) )
}
return result;
}
getPoint( t: number, optionalTarget = new BABYLON.Vector3() ) {
const point = optionalTarget;
const points = this.curve.getPoints();
const l = points.length;
const p = ( l - ( this.closed ? 0 : 1 ) ) * t;
let intPoint = Math.floor( p );
let weight = p - intPoint;
if ( this.closed ) {
intPoint += intPoint > 0 ? 0 : ( Math.floor( Math.abs( intPoint ) / l ) + 1 ) * l;
} else if ( weight === 0 && intPoint === l - 1 ) {
intPoint = l - 2;
weight = 1;
}
let p0, p3; // 4 points (p1 & p2 defined below)
if ( this.closed || intPoint > 0 ) {
p0 = points[ ( intPoint - 1 ) % l ];
} else {
// extrapolate first point
p0 = points[ 0 ].subtract(points[1]).add( points[ 0 ] );
}
const p1 = points[ intPoint % l ];
const p2 = points[ ( intPoint + 1 ) % l ];
if ( this.closed || intPoint + 2 < l ) {
p3 = points[ ( intPoint + 2 ) % l ];
} else {
// extrapolate last point
p3 = points[ l - 1 ].subtract(points[ l - 2 ]).add( points[ l - 1 ] );
}
if ( this.curveType === 'centripetal' || this.curveType === 'chordal' ) {
// init Centripetal / Chordal Catmull-Rom
const pow = this.curveType === 'chordal' ? 0.5 : 0.25;
let dt0 = Math.pow( BABYLON.Vector3.DistanceSquared(p0, p1), pow );
let dt1 = Math.pow( BABYLON.Vector3.DistanceSquared(p1, p2), pow );
let dt2 = Math.pow( BABYLON.Vector3.DistanceSquared(p2, p3), pow );
// safety check for repeated points
if ( dt1 < 1e-4 ) dt1 = 1.0;
if ( dt0 < 1e-4 ) dt0 = dt1;
if ( dt2 < 1e-4 ) dt2 = dt1;
px.initNonuniformCatmullRom( p0.x, p1.x, p2.x, p3.x, dt0, dt1, dt2 , this.tension );
py.initNonuniformCatmullRom( p0.y, p1.y, p2.y, p3.y, dt0, dt1, dt2 , this.tension );
pz.initNonuniformCatmullRom( p0.z, p1.z, p2.z, p3.z, dt0, dt1, dt2 , this.tension );
} else if ( this.curveType === 'uniform' ) {
px.initCatmullRom( p0.x, p1.x, p2.x, p3.x, this.tension );
py.initCatmullRom( p0.y, p1.y, p2.y, p3.y, this.tension );
pz.initCatmullRom( p0.z, p1.z, p2.z, p3.z, this.tension );
}
point.set(
px.calc( weight ),
py.calc( weight ),
pz.calc( weight )
);
return point;
}
}
export { CatmullRomCurve3 };
I didn’t properly test everything, I’m not an expert at this stuff and am probably going against some “good practices”.
But it works in my project and all my splines are correct now.
@bghgary
@bghgary , yes that are my findings:
Babylon only supports one type, the uniform indeed.
As far as I understand, the “uniform” type is the oldest one, but games tend to use the moderner versions like “chordal” and “centripetal”… but most often “centripetal”.
I have tested the “Hermite” solution but that was more trouble.
The thing is, there is a common use case for devs to want to just give a long list of points and then request the code to “draw me a long line through these 100s or 1000s of points”.
The Catmull-Rom curve offers just that (accepting long list of Vector3s).
While the Hermite spline on the other hand, doesn’t work like that (accepts only 2 points and 2 tangents).
I think it’s important for BabylonJS to have full support of a proper functioning Catmull-Rom implementation that simply accepts 1000s of points and just draws it, with no artifacts (which means, centripetal instead of “uniform”).
(and in my implementation, I also have to ability to provide a tension of 0 to 1 , which I’m not sure I have implemented correctly, but it is useable in its current form)
I’m not a github Babylon contributer yet ( considering I’ve only joined the 3D space just recently), so I’m not going to suddenly start editing the framework publicly just yet 
But if anyone wants to use my above solution for helping with updating the github code, feel free to just do so (obviously no credits or anything required): someone who actually knows what they are doing instead of me who’s just trying until it works  .
.
![]()
![]()
![]()
![]() ).
).![]() ).
).![]()